Which expressions represent rational numbers check all that apply – Which expressions represent rational numbers: check all that apply? This question invites us on an intellectual journey to explore the fascinating world of rational numbers. Join us as we uncover the secrets behind identifying rational expressions, unraveling the mysteries of number theory, and expanding our mathematical horizons.

In this comprehensive guide, we will delve into the concept of rational numbers, their unique characteristics, and the various forms they can take. We will equip you with the knowledge and tools to confidently recognize rational expressions, empowering you to navigate the complexities of mathematics with ease.

1. Definition of Rational Numbers

Rational numbers are numbers that can be expressed as a fraction of two integers, where the denominator (the bottom number) is not zero. They are also known as fractions. Rational numbers can be positive, negative, or zero.

Examples of rational numbers include:

• 1/2
• -3/4
• 0
• 1.5

Rational numbers differ from irrational numbers, which cannot be expressed as a fraction of two integers. Irrational numbers are non-terminating and non-repeating decimals.

2. Expressions Representing Rational Numbers

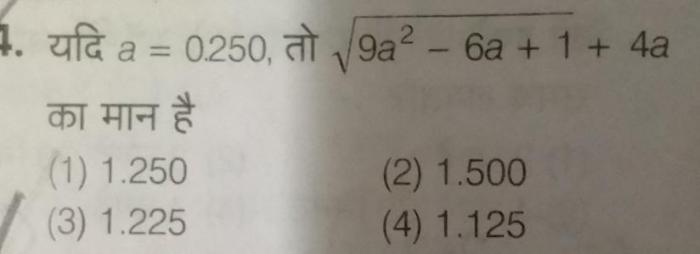
Rational numbers can be represented in various ways, including:

• Fractions:A fraction is a number that represents a part of a whole. It is written as two numbers separated by a line, where the top number (numerator) represents the part and the bottom number (denominator) represents the whole.
• Decimals:A decimal is a number that represents a part of a whole using a decimal point. It is written as a whole number followed by a decimal point and one or more digits.
• Percentages:A percentage is a number that represents a part of a whole expressed as a fraction of 100. It is written as a number followed by the percent sign (%)

To identify rational numbers in expressions, look for numbers that can be expressed as a fraction of two integers. For example, the expression “3/5” represents a rational number because it can be written as a fraction of two integers (3 and 5).

3. Methods for Determining Rational Numbers

There are several methods for determining if an expression represents a rational number:

1. Simplify the expression:If an expression can be simplified to a fraction of two integers, then it represents a rational number. For example, the expression “2/4” can be simplified to “1/2”, which is a rational number.
2. Check for repeating decimals:If an expression has a decimal that repeats, then it represents a rational number. For example, the expression “0.333…” represents the rational number 1/3.
3. Use the rational number theorem:The rational number theorem states that any number that can be written as a quotient of two integers (where the denominator is not zero) is a rational number. For example, the expression “sqrt(4)” represents the rational number 2 because it can be written as 4/2.

4. Examples of Rational Number Expressions: Which Expressions Represent Rational Numbers Check All That Apply

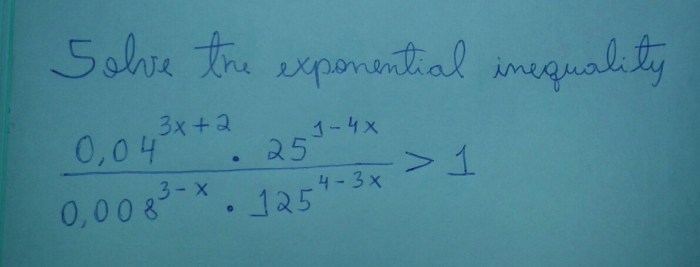
The following is a list of examples of expressions that represent rational numbers:

• Fractions: 1/2, -3/4, 5/6
• Decimals: 0.5, -1.25, 3.14
• Percentages: 25%, 75%, 100%

5. Exceptions and Special Cases

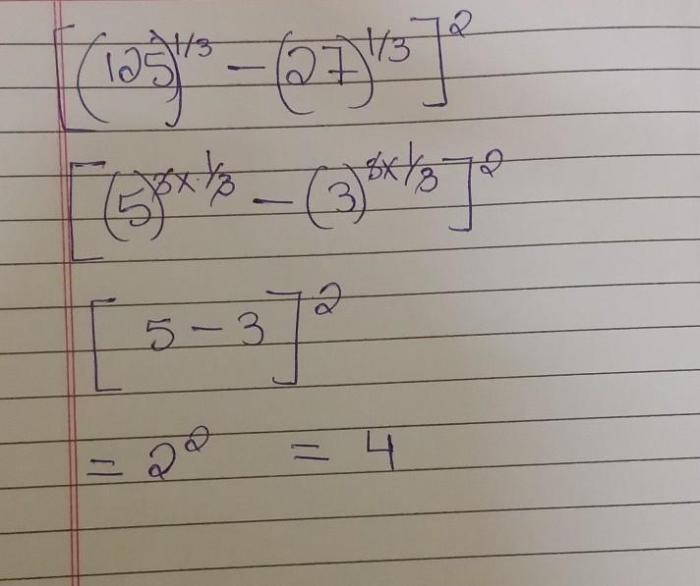
There are some exceptions to the rules for identifying rational numbers:

• Expressions involving variables:Expressions that involve variables may not always represent rational numbers. For example, the expression “x/y” is only a rational number if y is not equal to zero.
• Expressions involving complex numbers:Complex numbers are numbers that have both a real and imaginary part. Expressions involving complex numbers may not always represent rational numbers. For example, the expression “1 + 2i” is not a rational number because the imaginary part (2i) cannot be expressed as a fraction of two integers.

Questions and Answers

What are rational numbers?

Rational numbers are numbers that can be expressed as a fraction of two integers, where the denominator is not zero.

How can I identify rational number expressions?

Rational number expressions can be identified by their ability to be written as a fraction of two integers, or as a decimal that either terminates or repeats.

What are some examples of rational number expressions?

Examples of rational number expressions include: 1/2, -3/4, 0.5, 0.25, and 1.23456789.